Using AscRtain

Theoretical Motivation for Considering Collider Bias

Collider Bias and COVID-19

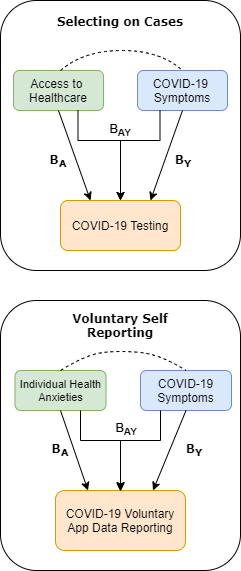
Arrows indicate effects of exposure $(A)$ and outcome $(Y)$ on selection into sample. Dashed lines indicate an induced correlation by conditioning on the sample.

Development

This app highlights some of the functionality of the R Package AscRtain developed by Gibran Hemani and Tom Palmer.

This RShiny app was created by Gareth Griffith as a pedagogical supplement to the MedRxiv preprint 'Collider bias undermines our understanding of COVID-19 disease risk and severity.' written with colleagues at the MRC-IEU, 2020.

Consider the scenario in which we want to test if a given exposure $(A)$ influences an outcome $(Y)$. Consider also that these two variables both independently cause a third variable $(S)$. Conditioning on $S$ will induce a relationship betweeen $A$ and $Y$. This is known as Ascertainment Bias or Collider Bias. Whilst it is largely acknowledged that sampling bias may affect representativeness of study findings, it is less well understood that conditioning on a collider may substantially bias the estimated association between an exposure and outcome.

Why is this particularly problematic in the analysis of COVID-19 data?
Because COVID-19 study participants are likely to be strongly non-random and if we consider $S$ to be selection into a COVID-sample then we condition on it by solely considering study participants. More worryingly, it is likely that exposure and outcome both predict entry into the COVID-19 samples, meaning we are conditioning on a collider and will produce biased estimates.

Take two major sources of COVID-19 data: COVID-19 cases and voluntary self-report:

We know COVID testing is non-random in the population. Factors associated with this non-randomness such as having pre-existing conditions, or being a key worker may plausibly predict both whether you receive a test and your risk of COVID-19. Similarly for self-reporting individual health-anxiety may plausibly predict both whether you opt into data collection and your risk of COVID-19.

If we estimate population associations based on these ascertained values our results and causal conclusions may also be biased.

Functionally this presents a problem as we cannot know the true effect of $A$ and $Y$ on sample participation. However, given known population frequencies for exposure and outcome, we can estimate possible selection effects which would give rise to observed outcomes under a true null. Depending on the range of values returned this allows us to make more informed inference about bias in our estimated associations.

Estimating over a plausible parameter space

This page demonstrates some of the functional utility of the AscRtain R Package. The parameter_space() function simulates values over the possible parameter space for selection into a study which could give rise to an observed OR between exposure and outcome. This plots the possible selection effects on exposure ($\beta_A$) and outcome ($\beta_Y$) which could give rise to a user-defined observed odds ratio (OR) under a true known OR of 1.

Population parameters are defined as follows:

$P(S=1)$ denotes the proportion of the population that is in the sample.
$P(A=1)$ denotes the proportion of the population for whom the exposure A is true.
$P(Y=1)$ denotes the proportion of the population for whom the outcome Y is true.
$P(A \cap Y)$ denotes the proportion of the population for whom A and Y are both true.

Selection effects are defined as follows:

$\beta_0$ denotes the baseline probability of being selected into the sample.
$\beta_A$ is the difference in probability of being selected into the sample given A=1 is true.
$\beta_Y$ is the difference in probability of being selected into the sample given Y=1 is true.
$\beta_{AY}$ is the difference in probability of being selected into the sample given both A=1 and Y=1 are true.

Observed Relationship

Observed OR

Unique Parameter Combinations (millions)

Population Parameters

$P(S=1)$

$P(A=1)$

$P(Y=1)$

$P(A \cap Y)$

Selection Effects

$\beta_0$ Range

$\beta_A$ Range

$\beta_Y$ Range

$\beta_{AY}$ Range

Estimated Parameter Combinations

Parameter Combinations plausibly giving rise to $P(S=1)$

Parameter Combinations plausibly producing observed OR

How does it work?

Under the Hood

Following Groenwold et al. (2019) we can calculate the biased OR for a binary exposure $(A)$ on a binary outcome $(Y)$ when both influence the probability of being present in the sample $(S)$.

Let us assume that being present in the sample is conditional on these two binary traits. We may then express an individual's chance of being present in the sample as a combination of four probabilities:

\[\mathbb{P}(S=1|A,Y)=\beta_0+\beta_AA+\beta_YY+\beta_{AY}AY\]

Where:

$\beta_0$ is the baseline probability of any individual to be a part of our sample. In order for any generalisation to be made, this needs to be non-zero, otherwise sampling is solely a function of the exposure and outcome.

$\beta_A$ is the differential probability of being sampled for individuals in the exposed group $(A=1)$.

$\beta_Y$ is the differential probability of being sampled for cases $(Y=1)$.

$\beta_{AY}$ is the differential probability of being sampled for cases in the exposed group $(A=1,Y=1)$.

Given this, we may derive the expected odds ratio, which gives:

\[E[\widehat{OR}_{S=1}]=\dfrac{\beta_0(\beta_0+\beta_A+\beta_Y+\beta_{AY})}{(\beta_0+\beta_A)(\beta_0+\beta_Y)}\]

A way to use this in a sensitivity analysis is to determine for a given fraction of population sampled $(pS)$, and known prevalence of outcome and sampling, what set of possible selection effects ($\beta*$) would give rise to a given odds ratio ($OR_{S=1}$) under a true null effect $(OR=1)$.

For the purposes of sensitivity analyses, we are solely interested in the $\beta$ parameter values that approximately give rise to our specified value of $pS$::

\[pS=\beta_0+\beta_Ap_A+\beta_Yp_Y+\beta_{AY}p_{AY}\]

Substituting in known values of $p_A$, $p_Y$ and $p_{AY}$ allows us to calculate $pS$ for a given $\beta_0$, $\beta_A$, $\beta_Y$ and $\beta_{AY}$. We then take all $\beta_*$ combinations which satisfy our $pS$ conditions, and calculate $E[\widehat{OR}_{S=1}]$ for all combinations. We can then present the combination of $\beta_*$ estimates which give rise to the bounds of $pS$ and the observed $OR$.

For any given $\beta_*$ values, we can simulate independent exposure and outcome data under selection pressures, and we should recapitulate our observed $OR$.

The AscRtain::parameter_space() function performs this analysis, and this shiny app is a wrapper for that function.

A simplified demonstration of this method is provided below. For a version of the example below taken directly from the literature see our preprint. For simplicity we omit discussion of the $\beta_{AY}$ interaction term here.

Smoking and COVID-19: A worked example

Let's take an example from the literature that emerged around smoking and COVID in the early stages of the pandemic, a preprint detailing a meta-analysis of 18 published studies of smoking and COVID-19 reported an OR for current smoking and hospitalisation of 0.17 (95% CI 0.13-0.21) amongst Chinese studies.

We have written explainers on why inferring from relationships from hospitalised patients may be subject to collider bias [1,2]. For the purposes of explanation here, let's assume that there is no interaction between the selection processes for smoking and COVID-19 into a hospitalised sample. That is, the selection forces acting on an individual who both smokes and has COVID-19 are equal to the sum of their constituent $\beta$ estimates.

To estimate plausible selection processes, we must input figures for $p_S$ (the proportion of the population sampled), $p_A$ (the population prevalence of smoking), and $p_Y$ (the population prevalence of COVID-19). We are exploring the chance of generating an OR of 0.17 under a null true relationship, thus there is no relationship between smoking and COVID-19, and so $p_{AY}$ is simply $p_Ap_Y$. We take $p_A$ from a population prevalence estimate of smoking in China (27.7%) [3]. We also assume COVID prevalence in the population at this point was 10%. Finally, we must provide a value for $p_S$. This is perhaps the strongest assumption, as we are unsure what fraction of the target population the 5023 individuals in the meta-analysis constitute, although for the purposes of this demonstration we will assume this represents 0.01 of the target population.

AscRtain Input

We can then input this into AscRtain for a binary collider structure using the parameter_space() function.

First we must initialise a new VBB (V-structure, Binary-exposure, Binary-outcome) structure

library(AscRtain)
x <- VBB$new
x()
#> <VBB>
#>   Public:
#>     clone: function (deep = FALSE) 
#>     histogram: function (bins = 30) 
#>     or_calc: function (b0, ba, by, bay) 
#>     param: NULL
#>     parameter_space: function (target_or, pS, pA, pY, pAY, b0_range, ba_range, by_range, 
#>     ps_calc: function (b0, ba, by, bay, pA, pY, pAY) 
#>     scatter: function () 
#>     scatter3d: function (ticktype = "detailed", theta = 130, phi = 0, bty = "g",

We can calculate an $OR$ if we input $\beta_*$ estimates.

x$or_calc(b0=0.1, ba=0.5, by=0.5, bay=0.2)
#> [1] 0.3611111

Now for given target odds ratio, we wish to explore whether the observed result could be explained solely by sample ascertainment. For this we use the AscRtain::parameter_space() function.

parameter_space() takes 10 arguments, which are as follows:

target_or is the observed $OR$.
pS is the proportion of the target population in the sample P(S=1).
pA is the proportion of the population who are in the exposed group P(A=1).
pY is the proportion of the cases in the population P(Y=1).
pAY is the proportion of the population who are both exposed and cases P(A=1, Y=1).
b0_range is the range of $\beta_0$ values we want to explore.
ba_range is the range of $\beta_A$ values we want to explore.
bay_range is the range of $\beta_{AY}$ values we want to explore.
granularity is the resolution of the $\beta_*$ ranges we wish to explore (default is 100).

For the result we suspect may be the result of an ascertained sample, we can input known population values.

x$parameter_space(
  target_or= 0.17,
  pS=0.01, 
  pA=0.277,
  pY=0.1,
  pAY=0.0277,
  b0_range=c(0,0.2), 
  ba_range=c(-0.1, 0.2), 
  by_range=c(-0.1,0.2), 
  bay_range=c(0,0), 
  granularity=200
)
#> 8000000 parameter combinations
#> 41784 within pS_tol
#> 762 beyond OR threshold

Which parameter values for selection effects give rise to an OR at least as extreme as 0.17 under a true null effect.

x$param
# A tibble: 762 x 9
#>      pA    pY    pAY     b0        ba       by   bay     ps1       or
#>   <dbl> <dbl>  <dbl>  <dbl>     <dbl>    <dbl> <dbl>   <dbl>    <dbl>
#> 1 0.277   0.1 0.0277 0.0131 -0.000503 -0.0126      0 0.0117  7.18e-15
#> 2 0.277   0.1 0.0277 0.0131 -0.00201  -0.0111      0 0.0114  2.04e-15
#> 3 0.277   0.1 0.0277 0.0131 -0.00352  -0.00955     0 0.0111  1.35e-15
#> 4 0.277   0.1 0.0277 0.0151 -0.00653  -0.00804     0 0.0125  1.26e- 1
#> 5 0.277   0.1 0.0277 0.0131 -0.00503  -0.00804     0 0.0109  5.61e-15
#> 6 0.277   0.1 0.0277 0.0101 -0.00201  -0.00804     0 0.00869 8.63e-15
#> 7 0.277   0.1 0.0277 0.0151 -0.00804  -0.00653     0 0.0122  1.26e- 1
#> 8 0.277   0.1 0.0277 0.0131 -0.00653  -0.00653     0 0.0106  5.31e-15
#> 9 0.277   0.1 0.0277 0.0121 -0.00503  -0.00653     0 0.0100  1.56e- 1
#> 10 0.277   0.1 0.0277 0.0101 -0.00352  -0.00653     0 0.00842 6.07e-15
# ... with 752 more rows

We can see that there are many values of $\beta_A$ and $\beta_Y$ which meet the target odds ratio. In order to get a feel for these, let's visualise them.

x$scatter()+ 
  ggplot2::geom_vline(xintercept=0, linetype="dotted") + 
  ggplot2::geom_hline(yintercept=0, linetype="dotted") + 
  ggplot2::ggtitle("Smoking and COVID-19 selection. beta_{AY} = 0")

We can see from the scatter plot above, that with relatively subtle changes in selection effects, we can induce ORs of a large magnitude. This example has excluded the possibility of the interactive effect on sample membership of both COVID-19 and smoking status, but this further complicates matters. There is a more comprehensive discussion of this in the medrxiv preprint that accompanies this app.

Let's go further - and investigate possible selection effects which could give rise to an OR indicating a 5-fold risk instead of a 5-fold protective effect of smoking on COVID-19 caseness. This can give us an indication of how sensitive our findings are to selection effects, which can help us interrogate the likelihood of our observed results generalising in external situations.

We can simply initialise another VBB with equivalent population prevalence estimates for A, Y and AY, but specify an observed OR of 5.

x1 <- VBB$new()
x1$parameter_space(
  target_or=5, 
     pS=0.01, 
     pA=0.277,
     pY=0.1,
     pAY=0.0277,
     b0_range=c(0,0.2), 
     ba_range=c(-0.1,0.2), 
     by_range=c(-0.1,0.2), 
     bay_range=c(0,0), 
     granularity=500
 )

SmokingColliderCombined <- x$param %>% 
        ggplot2::ggplot(., aes(x=ba, y=by))+
        ggplot2::geom_point(aes(colour=b0))+
        ggplot2::labs(colour = expression (paste("Baseline inc. prob. ", (beta[0]), " OR < 0.17"))) +
        ggplot2::scale_colour_gradient(low="darkgoldenrod2", high="white")+
        ggnewscale::new_scale_colour() +
        ggplot2::geom_point(data=x1$param, aes(colour = b0))+
        ggplot2::scale_colour_gradient(low= "blue", high="white")+
        ggplot2::labs(x = expression(paste("Effect of Smoking on inclusion probability (", beta[A],")")),
                      y=expression(paste("Effect of COVID-19 on inclusion probability (", beta[Y], ")")),
                      colour = expression(paste("Baseline inc. prob. ", (beta[0])," OR > 5")))+
        ggplot2::ggtitle("Smoking and COVID-19 Additive Selection Effects")+
        ggplot2::geom_hline(yintercept=0,size=0.2, linetype="dotted")+
        ggplot2::geom_vline(xintercept=0, size=0.2, linetype="dotted")

SmokingColliderCombined

We can see from the combined figure that there are a large range of possible selection values which could give rise to an observed relationship of a five-fold protective or risk-increasing relationship, under a true null effect. Remember, this is without including the possibility of interactive effects on participation for both exposure and outcome. It is also clear that these are highly sensitive to the specification of $\beta_0$, as the lower the baseline likelihood of sampling, the more likely it is that we are inducing relationships solely as a product of selection, as selected groups make up a larger proportion of the sample. We bounded this for the example above between 0 and 0.2, but it is clear that we only get such extreme ORs when $\beta_0$ is low. Unfortunately, $\beta_0$ is also one of the most difficult parameters to posit hypothetical values for as it is sensitive to study-specific sampling procedure and specification of target population. Moreover, these are often described in inadequate detail to parameterise this in secondary sensitivity analyses, which are most effective when carried out by primary researchers, to minimise researcher degrees of freedom.

We can explore the sensitivity of ORs to selection processes using the same process. If we hypothesise a two-fold elevated risk or protective effect of smoking and produce the same graphic, we can see how different selection processes must be between extreme and less extreme observed relationships. Below is the same graphic but with OR of 2 and 0.5 shaded.


x2 <- VBB$new()
x2$parameter_space(
  target_or=2, 
     pS=0.01, 
     pA=0.277,
     pY=0.1,
     pAY=0.0277,
     b0_range=c(0,0.2), 
     ba_range=c(-0.1,0.2), 
     by_range=c(-0.1,0.2), 
     bay_range=c(0,0), 
     granularity=500
 )


x3 <- VBB$new()
x3$parameter_space(
  target_or=0.5, 
     pS=0.01, 
     pA=0.277,
     pY=0.1,
     pAY=0.0277,
     b0_range=c(0,0.2), 
     ba_range=c(-0.1,0.2), 
     by_range=c(-0.1,0.2), 
     bay_range=c(0,0), 
     granularity=500
 )

x3$param %>% 
    ggplot2::ggplot(., aes(x=ba, y=by))+
    ggplot2::geom_point(aes(colour=b0))+
    ggplot2::labs(colour = expression (paste("Baseline inc. prob. ", (beta[0]), " OR < 0.5"))) +
    ggplot2::scale_colour_gradient(low="darkgoldenrod2", high="white")+
    ggnewscale::new_scale_colour() +
    ggplot2::geom_point(data=x2$param, aes(colour = b0))+
    ggplot2::scale_colour_gradient(low= "blue", high="white")+
    ggplot2::labs(x = expression(paste("Effect of Smoking on inclusion probability (", beta[A],")")),
                  y=expression(paste("Effect of COVID-19 on inclusion probability (", beta[Y], ")")),
                  colour = expression(paste("Baseline inc. prob. ", (beta[0])," OR > 2")))+
    ggplot2::ggtitle("Smoking and COVID-19 Additive Selection Effects")+
    ggplot2::geom_hline(yintercept=0,size=0.2, linetype="dotted")+
    ggplot2::geom_vline(xintercept=0, size=0.2, linetype="dotted")

We can see from the Figure above, that the less extreme the OR, the more subtle the selection processes can be - as selection effects producing an observed OR under a true null clearly extend further towards the centre for the twofold risk ratios, relative to the fivefold changes. For a given observed relationship we are essentially positing (in the additive space) that our selection processes fall into the central region of the graph, which diminishes as odds ratios become less extreme.

Simulate from parameter values to recapitulate target OR.

For proof of concept, we need to simulate individual level data in which there is no relationship between A and Y and demonstrate that we can recover the observed, biased OR solely as a function of differential selection pressures. Note that actual population size is not relevant here, it is the proportion of the population sampled that matters.

Parameters:

a <- subset(x$param, by==max(abs(by)))[1,]
a
# A tibble: 1 x 9
#>     pA    pY    pAY       b0      ba    by   bay    ps1    or
#>  <dbl> <dbl>  <dbl>    <dbl>   <dbl> <dbl> <dbl>  <dbl> <dbl>
#> 1 0.277   0.1 0.0277 0.000401 0.00220 0.115     0 0.0125 0.157

Simulate from parameters:

set.seed(1337)
n <- 1000000
Y <- rbinom(n, 1, a$pY)
A <- rbinom(n, 1, a$pA)
pS <- a$b0 + a$ba * A + a$by * Y
S <- rbinom(n, 1, pS)

What proportion of the population n are present in our sample S?

sum(S) / length(S)
#> [1] 0.012493

From our simulated population, what is the observed association between A and Y in the sampled subset?

summary(glm(Y~A, family="binomial", subset=S==1))$coef[2,1] %>% exp
#> [1] 0.1264771

Compare this to our expected biased association from x$param:

a$or
#> [1] 0.157

We can see that the OR is beyond the target OR that we specified in our research question. Thus we see an OR at least as extreme as our target OR within our sample, solely as a result of selection effects. In this case, if the baseline probability of being in the sample is 0.0004, and smoking increases this by 0.0022, whilst COVID-19 increases this by 0.115, we can find an OR of 0.157 for smoking on COVID-19 caseness, when the true relationship in the population is null. The same process will be true for all combinations of $\beta_0, \beta_A$ and $\beta_Y$ displayed in the scatter plot.

Useful Resources

Key References

Griffith, Gareth J., Tim T. Morris, Matt Tudball, Annie Herbert, Giulia Mancano, Lindsey Pike, Gemma C. Sharp, Tom M. Palmer, George Davey Smith, Kate Tilling, Luisa Zuccolo, Neil M. Davies, and Gibran Hemani. 2020. Collider Bias undermines our understanding of COVID-19 disease risk and severity. MedRxiv Preprint

Munafo, Marcus R., Kate Tilling, Amy E. Taylor, David M. Evans, and George Davey Smith. 2018. Collider Scope: When Selection Bias Can Substantially Influence Observed Associations. International Journal of Epidemiology 47 (1): 226-35.

Miguel Angel Luque-Fernandez, Michael Schomaker, Daniel Redondo-Sanchez, Maria Jose Sanchez Perez, Anand Vaidya, Mireille E Schnitzer. 2019. Educational Note: Paradoxical collider effect in the analysis of non-communicable disease epidemiological data: a reproducible illustration and web application. International Journal of Epidemiology, 48(2): 640-653.

Smith LH, and VanderWeele TJ. 2019. Bounding bias due to selection. Epidemiology. 30(4): 509-516.

Elwert, Felix, and Christopher Winship. 2014. Endogenous Selection Bias: The Problem of Conditioning on a Collider Variable. Annual Review of Sociology 40 (July): 31-53.

Cole, Stephen R., Robert W. Platt, Enrique F. Schisterman, Haitao Chu, Daniel Westreich, David Richardson, and Charles Poole. 2010. Illustrating Bias due to Conditioning on a Collider. International Journal of Epidemiology 39 (2): 417-20.

Groenwold, Rolf H. H., Tom M. Palmer, Kate Tilling. 2020. Conditioning on a mediator to adjust for unmeasured confounding OSF Preprint

Pedagogical Resources

The following apps give an informative introduction to collider bias in observational data, and allow the user to explore possible relationships.

Sensitivity Analysis for Selection Bias website. Smith LH, and Vanderweele TJ. 2019.
CollideR app. Luque-Fernandez et al. 2019.
Bias app. Groenwold, Palmer, and Tilling. 2019.

These R Packages allow a user to specify a DAG and simulate data from it, which can inform the size of bias for a specified model.
lavaan R Package Rosseel. 2012.
dagitty R Package Textor et al. 2016.
simMixedDAG R Package